Sam H. Jones
The earliest references to tidal differences were made by the Greek astronomer and explorer
Pytheas
around 330 B.C. On a voyage to the British Isles he observed the great ocean tides there. The tidal differences were much greater than those found in his native Mediterranean. He discovered that there was some sort of relationship with the moon. Pytheas not only discovered that there were two high tides per lunar day, but also that the amplitude depended on the phases of the moon.
The Mediterranean did not provide a good observatory for tidal theory because the amplitude (magnitude) of the tides was not as pronounced there. About 150 B.C.
Seleukos
made observations in the Red Sea. He found that the two tides per day had unequal amplitudes when the Moon was far away from the equator.
The Greek geographer Strabo quoted the early Greek scientist, Poseidonios in a book written around the year 23 A.D. Poseidonios made studies of the tides of the Atlantic coast of Spain around 100 B.C. Quoted from Strabo’s book is the oldest existing text describing the tidal phenomenon of diurnal inequality.
When the moon rises above the horizon to the extent of a zodiacal sign (30°), the sea begins to swell, and perceptibly invades the land until the moon is in the meridian; but when the heavenly body has begun to decline, the sea retreats again, little by little; then invades the land again until the moon reaches the meridian below the earth; then retreats until the moon, moving round towards her risings, is a sign distant from the horizon … The flux and reflux become greatest about the time of the conjunction (new moon), and then diminish until the half moon; and, again, they increase until the full moon and diminish again until the waning half moon. If the moon is in the equinoctial signs (zero declination), the behavior of the tides is regular, but, in the solstitial signs (maximum declination), irregular, in respect both to amount and to speed, while in each of the other signs, the relation is in proportion to the nearness of the moon’s approach.
1
The phenomenon of the diurnal inequality is illustrated in figure 1:
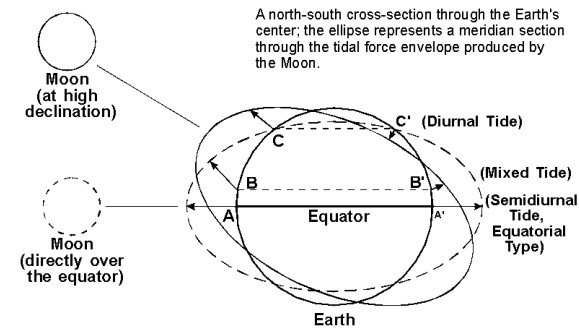
Figure: 1. (source: http://co-ops.nos.noaa.gov/restles4.html)
More than two thousand years ago the ancient Greeks, as with many other phenomena, made astute observations about the world around them. As with many of their other observations they did not fully understand or explain the cause. It would take another 1600 years before the tides’ motions would be more fully understood. In the meantime, there were several unsuccessful attempts at explaining the various phenomena.
An English monk in the 8
th
century discovered the phase lag of the ocean tides, noticing that each port along the British coast had its own tidal phase. Although Bede the Venerable’s observations were accurate, he attributed the ebbing tide to the Moon “blowing” on the water and flowed again when the Moon moved a bit.
Ekman attributes the first scientific attempt to explain the tidal phenomenon to an Arabian scientist in the 13
th
century. It is claimed that the sun and the moon heat the waters, thereby making them expand. In Zakariya al-Qazwini’s own words:
-
As to the rising of the waters, it is supposed that when the sun acts on them it rarefies them, and they expand and seek a space ampler than that wherein they were before, and the one part repels the other in the five directions, eastwards, westwards, southwards, northwards, and upwards
2
.
The hypothesis failed to explain why the moon, not the sun, played the leading role. The whole idea that the sun and moon played a role at all was sometimes difficult to grasp. According to one idea, the tides were caused by the great whirlpool known as the Maelstrom off the coast of Northern Norway. We know today that there is a connection between the whirlpool and the tides, but it is the tide that causes the whirlpool and not the other way around.
With the recent rediscovery of America, in the mid 16
th
century it was suggested by an Italian scientist that in addition to the effect of the moon, the sea water was oscillating between the coasts of America and Europe. Apparently this type of resonance had been observed in some of the larger local lakes.
Moving into the 17
th
century, Johannes Kepler was convinced that the tides depended on the moon and the sun. He believed that there was some attractive force, something like magnetism. Galileo was surprised that Kepler “became interested in the action of the moon on the water, and in other occult phenomena, and similar childishness”
3
. Galileo himself believed the Copernican theory positing that the tides were produced by the combined effects of the earth’s rotation around its axis and its orbital motion around the sun. These motions would set the water on Earth into oscillations observed as tides. He used a thought experiment where the water in a container may be made to oscillate by acceleration and slowing of the container or pan. He concludes that the same must hold true for the vast oceans.
Rene Descartes, slightly after Galileo, had his own ideas. The Cartesian vortex will also be discussed as an explanation for the planetary motions. Both the moon and the earth, in this theory, were surrounded by a large vortex. The pressure exerted by the vortex of the Moon on the Earth’s surface caused the tides to rise. Unfortunately, the theory incorrectly predicts a low tide when in reality there is a high tide.
The debate continued through the 17
th
century and became quite confusing. What sort of force could cause the oceans to behave in such a way? If the Sun and the Moon were not exerting their influence, through some occult force or otherwise, how could one explain the observations?
An explanation came later in the 17
th
century with Isaac Newton’s Principia. Universal gravitation was not only causing the apple to fall to the Earth. It was holding the planets in orbit, and also causing the tides because of the varying distances from the Sun and the Moon. In Newton’s words:
-
But let the body S come to act upon it (the globe), and by its unequable attraction
-
the water will receive this new motion. For there will be a stronger attraction upon
-
that part of the water that is nearest to the body, and a weaker upon that part which
-
is more remote.
Newton’s theory was able to explain the three fundamental properties of the tides: the main period of 12 lunar hours, the dependence of the amplitude on the lunar phases, and the diurnal inequality. Figure 1 illustrated the diurnal inequality. Figure 2 illustrates the effects of the lunar phases:
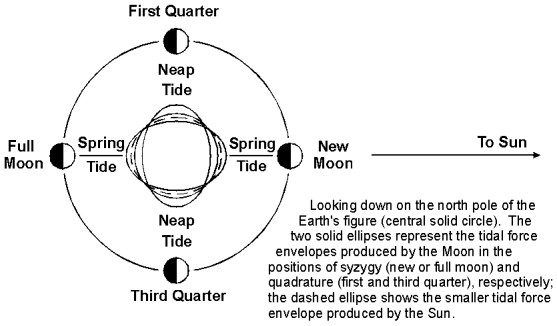
Figure: 2. (source: http://tidesandcurrents.noaa.gov/restles3.html)
While Newton’s theories were pivotal in providing the foundation for the development of a mathematical treatment of tides, they were by no means the end of the story. Later mathematicians built upon Newton’s epoch-making discoveries much in the same manner that Newton stood on the shoulders of giants in making his discoveries. Such is the nature of scientific discovery. The lunar constituent which produces the twice daily tides is illustrated in figure 3.
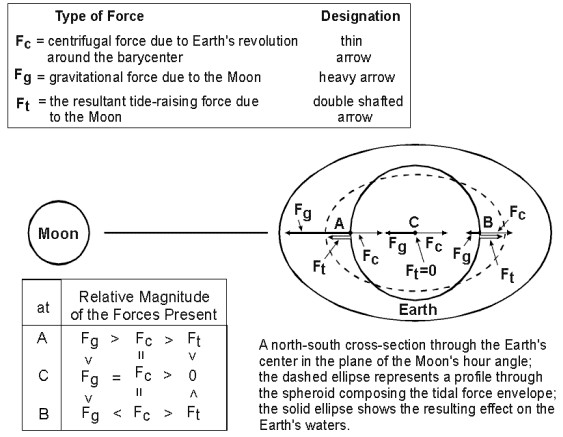
Figure: 3. (source: http://tidesandcurrents.noaa.gov/restles3.html)
It was not until the second half of the 18
th
century that a mathematical formula was fully developed by Pierre de Laplace. The tidal potential was described by Laplace in the following manner:
The three preceding terms give rise to three different types of oscillations. The periods of the oscillations of the first type are very long; they are independent of the motion of the earth, and depend only on the motion of the celestial body L in its orbit. The periods of the oscillations of the second type depend mainly on the rotational motion t of the earth; they are approximately one day. Finally, the periods of the oscillations of the third type depend mainly on the angle 2t; they are about half a day
4
. The constituent causing the semi-diurnal tide, centrifugal force, is further illustrated in figure 4:
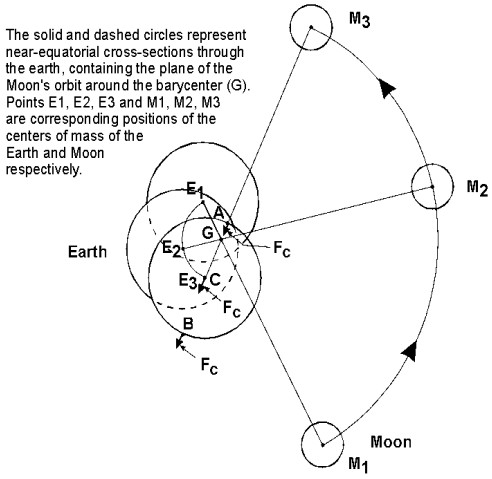
Figure: 4. (source: http://tidesandcurrents.noaa.gov/restles3.html)
The importance of Laplace’s equations should be emphasized. In addition to providing a mathematical model, he was the first to treat ocean tides as a problem of water in motion instead of water in equilibrium. His equations describing ocean tides could not be solved in practice until the invention of the computer.
For purposes of this unit we will deconstruct Laplace’s tidal formula to teach students about periodic functions. Each of the functions will be treated in a discrete manner. If time permits, the students may be introduced to the composite functions. For a more advanced course this unit could be expanded to include Fourrier series in addition to the equations found in this unit. The discrete functions are shown in figure 5:
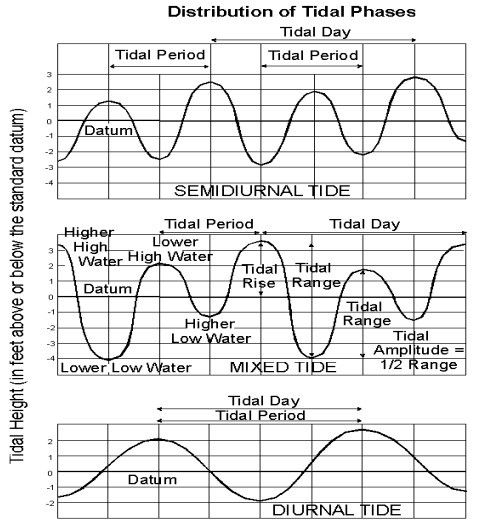
Figure: 5. (source: http://co-ops.nos.noaa.gov/restles4.html)
The primary tidal constituents (ie, the discrete functions), along with their conventional designations are listed below. This table will be useful in understanding the discrete periodic functions which describe the tides.
The following are among the
major tidal constituents
contributing to the astronomical tide:
M
2
- Principal lunar semidiurnal constituent (speed: 28.984 degrees per mean solar hour)
S
2
- Principal solar semidiurnal constituent (speed: 30.000 degrees per mean solar hour)
N
2
- Larger Lunar elliptic semidiurnal constituent (speed: 28.440 degrees per mean solar hour)
K
1
- Luni-solar declinational diurnal constituent (speed: 15.041 degrees per mean solar hour)
O
1
- Lunar declinational diurnal constituent (speed: 13.943 degrees per mean solar hour)
M
4
- First overtide of M
2
constituent (speed: 2 x M
2
speed)
M
6
- Second overtide of M
2
constituent (speed: 3 x M
2
speed)
S
4
- First overtide of S
2
constituent (speed: 2 x S
2
speed)
MS
4
- A compound tide of M
2
and S
2
(speed: M
2
+ S
2
speed)
To better facilitate an understanding there may be a demonstration or a directed activity of a tide machine. Students should have some understanding of the trigonometric functions as circular functions. My students have used JAVA applets such as the ones found at http://www.ies.co.jp/math/java/trig/index.html.
Lord Kelvin invented a tide machine to handle complex calculations. It utilized a series of wheels and pulleys to sum the various functions. A demonstration of the machine using a JAVA applet may be seen at: http://www.ams.org/featurecolumn/archive/tidesIII3.html
The United States Coast and Geodetic Survey tide- predicting machine No. 2 was designed by Rollin A. Harris and E.G. Fischer and constructed in the instrument shop of the U.S. Coast and Geodetic Survey. It was completed in 1910 and replaced the Ferrel Tide-Predicting Machine in 1912. The machine summed 37 constituents and was capable of tracing a curve graphically depicting the results.
5