Shaunquetta N. Johnson
Connecting Math and Literacy
Picture books are wonderful resources and teaching tools to utilize across all academic areas, but they are particularly useful in teaching fractions. Teachers can read picture books at the beginning of a lesson to capture students' attention and gain enthusiasm for the lesson topic. Picture books are great in providing vivid illustrations with minimal text to explain vocabulary and challenging concepts. Students can use picture books to reinforce skills they find difficult or review skills they haven't practiced in a while. Additionally, children may find pleasure in reading a picture book for enjoyment. There are a plethora of books about fractions and how to teach the topic. I included a comprehensive list of picture books that connect literacy to learning fractions. Teachers are encouraged to build a math library with the recommended titles as well as with other titles not mentioned. The books I've included will help teach fractions, define key terms used in studying fractions and explain how to manipulate fractions within the constructs discussed later in the unit.
Teachers must first understand what they are teaching. Like students, teachers must rely on schema but push aside any negative memories, if any, about learning fractions. Elementary teachers are taught basic concepts and strategies for teaching fractions. Unlike high school teachers who are taught in-depth content and procedures, elementary teachers have to independently research challenging subject matter to become familiar and comfortable with teaching difficult concepts.
"Children learn mathematics through the use of language."
2
Vocabulary and key words are introduced orally through discourse during math lessons and with other students during practice. Through the use of language students begin to understand operations, mathematical processes, and the names of figures, shapes, and symbols used in everyday math. In order to enhance comprehension and mastery, students must also have a pictorial representation to explain and justify their work. It is true for elementary grades that there is a natural connection between children's literature and mathematical concepts.
3
Children's literature infused during math time is critical in developing "math sense" in students. Shatzer cites Whiten and Wilde stating, "Literature motivates students to learn, provides a meaningful context for math, celebrates math as a language, demonstrates that math develops out of human experience, fosters the development of number sense, and integrates math into other curriculum areas."
4
In essence, literature is required in all subject areas, and picture books complement and supplement lessons to develop students' thinking and learning. It is essential that teachers build a library not only for literacy blocks but for all content area subjects. High-quality books are necessary for development.
Children's literature is a driving force for giving students a "meaningful context for learning mathematics as it helps learners value mathematics, encourages [them] to become mathematical problem solvers. . . [and] to communicate mathematically, supports . . . reasoning mathematically, and explores a variety of mathematical topics."
5
Picture books engage student and provides visualizations of math concepts in illustrations. Children are better at explaining their reasoning and strategies which resulted in math becoming more enjoyable. Students are more persistent with difficult tasks and increased in internalizing more about what they learned to experience success. Teachers must link literature and numeracy in an interactive and meaningful way in order for students to understand math concepts and sustain the knowledge. Research supports higher math scores when strategies are combined with literature.
6
Understanding Fractions
Fractions have always been considered as a daunting challenge for students. One explanation of why fractions are not well understood by young learners is because there is a lot to know about them, from part-whole to ratios to division and other mathematical operations. It is critical to connect visual representations with procedures (adding, subtracting, multiplying, dividing, etc.) in order to process and master fractions. Students seem to prefer to draw circles to represent fractions rather than squares, rectangles or any other shape.
7
Moreover, teachers need to provide multiple opportunities and various strategies to work with fractions.
In learning about fractions, the part-whole construct of rational numbers and the process of partitioning are the fundamental developments of understanding the four subordinate constructs of fractions. Priority has been given to learning the concept of part-whole in understanding fractions, and has been the traditional base to introducing the other constructs in lower elementary grades.
8
Secondly, the ratio construct has been noted as the most "natural" step to promote the concept of equivalence and subsequently the process of distinguishing equivalent fractions.
9
The third construct, operator, is helpful for developing an understanding of the multiplicative operations of fractions. The quotient measure is used for division. The fifth construct, measure, is considered a necessity for the development of additive operations of fractions.
10
Ultimately, the perquisite for solving problems in the domain of fractions is a sound understanding of all five constructs.
Charalambous and Pitta-Pantazi, along with Van de Walle, thoroughly define the five fraction constructs, and I provide a pictorial representation to explain each construct.
The Part-Whole Construct
"Part-whole construct is a continuous quantity or a set of discrete objects split into parts, of equal size."
11
Part-whole can extend into "part of a group"
12
(ex. part of a class) or part of a length (running 2 ½ miles). The part-whole fraction "represents a comparison between the number of parts in the split unit to the total number of parts in the entire unit. As an end result, the numerator of the fraction is less than or equal to the denominator."
13
"A circle model is most effective in displaying the part whole relationship. Part-whole is much more than shading an area of a circle."
14
Figure 1. shows two examples of part-whole

There are four parts to the whole, and two parts are shaded red, two parts, white.
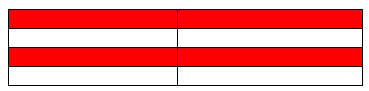
Two-fourths are shaded red. Each row is considered one part. There are four rows. There are two rows shaded red.
The Ratio Construct
The ratio construct is represented as "part-part or part-whole."
15
A ratio compares two quantities and is considered as "a comparative index rather than just a number."
16
Additionally, a ratio can mean probability, the chance or likelihood of an event occurring. For example: ¼ means 1 out of 4 girls like baseball or whole probability. It could translate into comparing girls who like baseball (part) to those who do not like baseball (part); or girls who like baseball to those in (part) the class (whole). Students must pay attention to context in order to understand how to successfully represent this fraction in picture.
17
Figure 2. illustrates ratios

For every moon there are 3 stars. The ratio is 1:3. In fractional terms ¼ is moon and ¾ are stars. If there are 2 moons, there are 6 stars. The ratio is 2:6. In fractional terms 2/8 are moons and 6/8 are stars.

The Operator Construct
The operator construct indicates there is an operation to perform when manipulating a fraction. For example ½ of 10 sq. ft. or 1/3 of the class reading silently. These two examples indicate a fraction of a whole and "students may be able to use mental math to determine the answer." This construct receives some emphasis, but not enough. And "knowing how to represent fractions doesn't" equate to students "knowing how to operate with fractions."
18
Figure 3. shows the operation of either subtracting or dividing. Jane is either subtracting from her pile or dividing between her brother and herself.
Jane's marbles

Jane had 6 marbles. She gave ½ to her little brother. How many does Jane have left?
Since there are 2 people, Jane and her brother, and 6 marbles, both will get equal amounts. Jane will have three left.
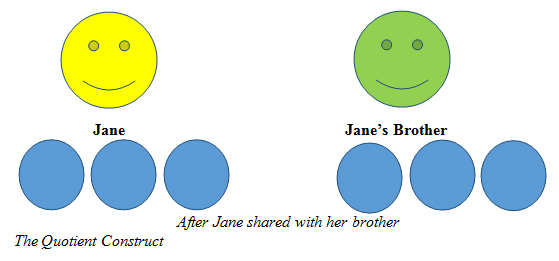
The quotient construct is synonymous with the term division construct. This construct is not a part-whole situation, but relates to the fraction in term of dividing. For example, $30 is shared amongst 4 people. Each person receives ¼ of the money, or $7 ½ dollars. Unfortunately division is rarely connected to fractions. Students should have a sense and "feel comfortable" with fractions represented in division.
19
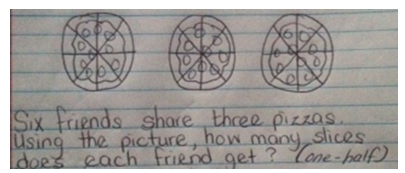
Figure 4. demonstrates how six friends share three pizzas. Each friend gets 4 slices which is ½ of a whole pizza.
The Measure Construct
The measure construct "focuses on how much rather than how many parts." A length is identified "as a measurement piece to determine the length of an object." For example: in the fraction 4/7, the unit fraction 1/7 is the selected length to "count or measure to show that it takes 4 of those (1/7) to reach 4/7." The measure construct is most associated with using the number line or other measuring tools (rulers) to determine the length from one point to another.
20
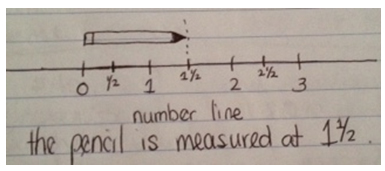
Figure 5. illustrates a number line with fractions
Pictures and math problems are used as strategies to gain students' attention. Pictures are used to engage students in the lesson and maintain their attention during the lesson. After capturing their attention, students can begin to perceive and explain the details seen in the pictures. Problems in math generate thinking, therefore eliciting students' attention to solve an equation.
21
Fractions and Elementary Students
Teaching Fractions
The concrete-representational-abstract strategy (CRA) is used during instruction with individual students and a small or whole group. The CRA strategy is implemented in three steps in which the first step concentrates on modeling and teaching math skills with concrete materials. Base-ten blocks, cubes, pattern blocks, colorful bears, chips, geometric shapes, fraction bars/circles are examples of concrete materials students can manipulate to learn math concepts. In the representational stage, math skills are demonstrated through drawing pictures. Drawings can consist of replicas of the concrete objects, tally marks, shapes, or other small objects. The last step is abstract in which signs, symbols, and numbers are introduced and used to solve equations and word problems. Students should learn the math skills at each stage before progressing to the next. Students are encouraged to continue use of concrete objects and pictures in the abstract stage to enhance mastery. The key to the CRA strategy is to ensure students learn how to visually represent math skills using manipulatives and pictures to explain their thought processes.
One possible solution to aid students with learning fractions is creating and using math journals. A math journal will organize students' thinking, provide space to link vocabulary with pictorial representation, and give students a visual representation to explain challenging math concepts, rules, procedures and operations. Math journals are great supplements to help visual learners to understand and learn math through images. Several educational resources such as Pearson Education, teachersvision.com, etc. encourage teachers to utilize journals during math. Students can create a math journal to record thoughts, observations, and experiences. Math journals become tools students rely on to capture what they're learning. Math journals are not only beneficial to visual learners, but can also motivate low achievers and reluctant learners. Low achievers and those learners who are reluctant to participate, may find it beneficial to document their learning through drawing, using symbols, and keywords (very minimal) in a journal.
22
The key to using math journals is taking a few minutes for students to illustrate their learning rather than rushing a lesson and moving on to another when understanding of the present concept(s) has yet to be achieved. Teachers must model how to create and use math strategy journals to solve math problems by drawing pictures, symbols and creating charts, graphs, and tables.
23
Gunderson and Gunderson suggest to write out the fraction words rather than in standard notation at the commencement of fraction instruction.
24
For example, teachers should write out three-fourths instead of writing the number fraction ¾. This is consistent with teaching students the abstract stage last. After writing out the words
three-fourths
, a simple fraction picture can accompany the fraction word for a more clear understanding.
Practicing Theory
The theory of looking versus seeing is a powerful tool that teachers must utilize when teaching students how to focus on and analyze fraction images. The idea of looking at an image is naming basic details and attributes visible to the eyes. Looking is an act of choice to gain information about an image's physical and surface appearance, and seeing entails a deeper thought process than looking. The concept of seeing involves meaning and interpretation. Seeing requires an analysis of the image to fully capture what the image is about.
25
In order to gain a deeper understanding of fractions, students must learn the constructs and begin to see the relationship of fraction images to other fraction images and fraction words. Students must begin to see that fractions are divided into equal parts and apply this concept to finding equivalent fractions and comparing fractions. If the parts are unequal, then it becomes impossible to determine if fractions are equal to each other. The importance of seeing the relationships between fractions and their parts determines how successful students are in solving problems of equivalency and comparison.