Elizabeth M. E. Nelson
Currently teaching a class of 26 emerging bilingual first graders in New Haven Public Schools, I am using
The Math In Focus: Singapore Math Curriculum
and have found that it is failing to meet the needs of my diverse population of urban students. One foundational philosophy of the
Math In Focus (MIF) Curriculum
is working with the idea that students transition from concrete to pictorial to abstract representations (see Figure 1) of their mathematical thinking. As with many curricula,
MIF
suggests the use of manipulatives to help facilitate students' concrete representations and, of course, the use of universal numbers and symbols to facilitate abstract representations that can be easily communicated with others at this level of understanding. One component of
MIF
that may not be as common in other curricula is the use of pictorial representations, focusing mainly on number bonds (see Figure 1) in first grade and bar models in upper grades. The number bond consists of two circles being connected with one line each to another circle. This is intended to symbolize the two parts (7 and 3, in Figure 1) used to compose the whole (10, in Figure 1). This symbolic representation of a concept continually proves to be unhelpful and confusing for the majority of my students. The
MIF
curriculum makes the claim that "clear and engaging visuals that present concepts and model solutions allow all students regardless of language skills to focus on the math lesson."
2
From my experience, these pictorial representations may help some students, but have been a source of confusion for the majority of my emerging bilingual students, regardless of whether or not the instruction is provided in their native language.
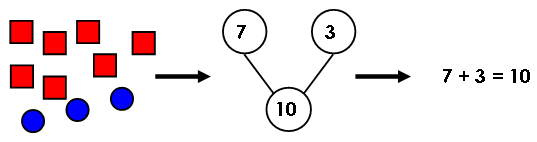
Figure 1: Concrete (blocks) --> Pictorial (example of a number bond) --> Abstract
Throughout the
MIF
curriculum, the order in which different concepts are introduced, the manner in which they are presented, and the tasks given to the students make it difficult for them to master math CCSS. For example, an initial focus is placed on teaching students how to use curriculum-prescribed number bonds rather than developing strategies to add or subtract. The later focus on using strategies to add and subtract is limited and teacher-centered. The formatting of the curriculum suggests that the teacher should explicitly teach and "model" the strategies; and then, through guided and independent practice, the students should use the prescribed strategy. The addition strategies include "counting on" and "using number bonds." Meanwhile, the subtraction strategies include "taking away," "counting on," "counting back," and "using number bonds." No other strategies and no suggestions to have students share their ideas are presented in the curriculum. Furthermore, the tasks that students are asked to do generally involve simply recording the answer. The suggestions in
MIF
have done little to lead to
students
to effectively develop, discuss, and choose efficient strategies as needed to meet the math CCSS.
Despite priding itself on mirroring the practices used in the mathematical powerhouse of Singapore, the
MIF
curriculum is like the majority of the math curricula sold in the United States, as it uses a behaviorist approach. I believe that this heavy reliance on behaviorist theory is one component that is doing a huge disservice to our students. The presumption of behaviorist theory is that our students are "empty vessels" and that our job, as teachers, is to fill them up with facts. While I have certainly met my share of teachers who will openly state that "our students come to school with
nothing
," I also know that the majority of the teachers I've worked with believe that their students' background knowledge, experiences, and interactions with others are all powerful learning tools. If this is the case, why do we continue to teach math in a way that assumes that the only way for the child to learn is through the direct teaching of skills by the teacher? Those of us who believe children construct knowledge through meaningful experiences and through interactions with peers and adults have a more constructivist or social constructivist view of learning. Most math curricula do not take these views into account, so there is room to expand curricula and classroom practices in order to foster a constructivist approach.
While agreeing with and working with the understanding that students benefit from understanding concrete representations before pictorial representations, and pictorial representations before abstract representations, I would like to argue that using student-created pictorial representations will help to further promote children's mathematical thinking. These representations would certainly be more meaningful to the students given that they will be the ones involved in developing them. Being given the task to focus on representing the process or strategy used instead of focusing simply on recording the product will help students to use metacognitive skills and further construct their concepts of addition and subtraction. Also, pictorially representing the
process
may help to facilitate the transition to the abstract representations of the symbols ("+" and "-") that represent processes. Furthermore, having a pictorial representation of their process will likely help students with limited language skills or those struggling to share and explain their strategies to do so. Through sharing their strategies with their class, all students will be exposed to a variety of strategies that they may be interested in trying to implement, while also having the opportunity to compare strategies for their accuracy and efficiency. Likewise, teachers will be both enlightened as to where their students stand with their problem-solving skills and provided with more information that they can subsequently use in order to challenge students or to help uncover misconceptions that may have otherwise gone unnoticed.
This unit also encourages teachers to hold more asset-based perspectives, rather than deficit-focused perspectives: it attempts to inspire teachers to help each student to use and represent what they already know as a way to help improve their mathematical thinking. A review of research on and examples of student-created pictorial representations will help teachers to look at students' "drawings" through a new lens. Ideally this unit will also help to spark professional conversations about how what we learn from students can influence our instruction and differentiation. Through providing ideas on how to facilitate using students' pictorial representations during math—as well as strategies on how to help students transition from concrete, to pictorial, to abstract representations of addition and subtraction—I hope to provide tools that will result in students being better equipped to meet the high Common Core State Standards. Ultimately, I also hope to influence changes in practice that will result in students being able to independently use higher-order mathematical thinking when approaching math problems throughout their school years and beyond.