Elizabeth M. E. Nelson
The collection of research, teaching strategies, and sample activities that follow are not intended to be merely part of one collective unit. Rather, teachers can use them to promote mathematical thinking throughout the year. By implementing many of these strategies to supplement current curricula, teachers will be better equipped to meet the demands of the math CCSS, particularly within the strand of "Operations and Algebraic Thinking," as well as Mathematical Practices."
3
Rationale: Why use students' pictorial representations?
When considering the need for students to think mathematically, most experts agree that language is an absolute necessity. As NYU professor of journalism and mass communications Mitchell Stephens notes, "to be human...is to use and understand words. Most of what we can sense, feel or imagine we can express through language."
4
However, the question arises: Do we need language to be able to think? Without language, many would argue that thinking, particularly higher-order thinking, is simply not possible. According to American cognitive psychologist Elizabeth Spelke, humans' unique communication tool of language not only allows us to exchange information with other people, but also serves "as a mechanism of communication between different systems within a single mind."
5
In accordance with this theory, if we want to ensure that our students are thinking mathematically, we inevitably need to make sure that we are helping facilitate the language that allows these types of thought processes to occur.
Yet, if language is so important, why not just ensure that students are given ample opportunities to develop their spoken or oral language? Educator Dr. Susan Sheridan has done integrated research dealing with markings from 1.9 million years ago and "neuroconstructivist" theories. Connecting these theories to the present, she has suggested:
-
Since humans still use images to express thought, and, in fact, require images
-
to understand their most complicated, abstract thoughts, it is clear that words
-
have not replaced the power of drawings to express meaning, and, most
-
probably, never will.
6
Based on the above observations and conclusions, we can certainly work with the assumption that written and spoken language can work in tandem to help further develop children's language skills, as well as their mathematical thinking skills.
Having established that productive language (including speaking and writing) can certainly be capable of helping to promote mathematical thinking skills, it is important to look at how this concept is reflected and supported within our standards and curriculum. Within the domain of "Operations and Algebraic Thinking" of the CCSS, the first-grade standards involve students being able to "solve word problems...by using objects, drawings and equations...to represent the problem."
7
The philosophy of the
Math in Focus
curriculum closely mirrors this standard by approaching solving problems concretely (with objects), pictorially (with drawings), and abstractly (with equations).
8
While I applaud
MIF
curriculum's attempt to scaffold instruction by implementing components of the Concrete-Representational-Abstract (CRA) Instructional Approach
9
, its use of number bonds limits or impedes students' learning and conceptual understanding. When given the outline of the number bond and being asked to fill it in, students are simply not representing their own concrete understanding, and using this "pictorial representation" does nothing more than fail to support children's mathematical thinking. As a result, the number bonds become just another circle to fill in on a worksheet, which founders of the international Children's Mathematics Network, Worthington and Carruthers, criticize as being "to mathematics that 'painting by numbers' is to art."
10
They prevent children from representing their own mathematical thinking and, therefore, limit the power that pictorial representations can have in helping a student understand the transition from concrete to abstract representation.
When considering the problem that the majority of math curricula do not have adequate opportunities for students to effectively transition from concrete to abstract representations in a way that preserves their personal, mathematical thinking, I would like to suggest taking the lead from the practices of emergent literacy. As is done with emergent literacy, in emergent mathematics emphasis should be placed on students creating representations that are meaningful to them. In three separate studies looking at students' representations in problem solving, Woleck, Nicol and Saundry, and Smith found that first-, second-, and third-grade students, respectively, used their pictorial representations as functional tools for problem solving or as a way to represent their thinking or a solution.
11
When encouraging students to use their own pictorial representations, whether used as placeholders for concrete objects or as a form of communicating, teachers will inevitably help to facilitate mathematical thinking and understanding. While using students' pictorial representations at any level can be beneficial, evidence suggests that it is the most critical in the early elementary years.
For those who have limited experiences with emergent writing or with having students develop their own pictorial representations, it may be challenging to know what to expect from early elementary students' self-created representations. According to Carruthers and Worthington, within mathematics students may be creating and reading back dynamic, pictographic, iconic, written or symbolic marks. Dynamic representations are marks that students make that mainly show a change or activity. When students provide representations that are drawings resembling something that is in front of them, they are making pictographic marks. Iconic marks differ in that they use one type of iconic form (often tallies, circles, stars, etc.) to represent each item when counting. When students use written graphics, they are writing out their thoughts (or approximations of such) using letters and words. Finally, students can also use symbolic marks, which involve the abstract numbers and symbols of operations earlier referred to. While most children's graphics will develop in this general order, these areas are not necessarily sequential or mutually exclusive.
12
While to the inexperienced / untrained eye, some children's marks (see Figure 2) may look quite idiosyncratic, it is important to keep in mind that if you listen to the child's explanation of his or her representation or observe his or her process in creating one, you will likely uncover a wealth of thinking.
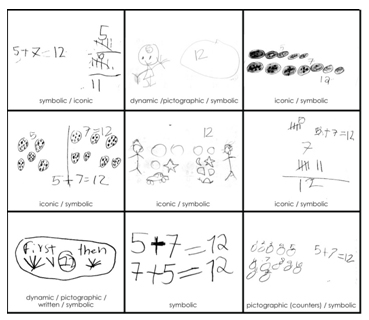
Figure 2: Samples of students' pictorial representations for the story problem:
María has 5 cookies. Alondra has 7 cookies. How many cookies do they have in all?
Of the variety of marks outlined above, the form or combination of forms that a child uses are influenced by his or her past experiences and background knowledge. This prior information may be from home or school or from interactions with peers. By bridging this information, the processes of understanding and finding meaning in the gradual and newly acquired information on abstract symbols will help develop a child into what Carruthers and Worthington have coined as "binumerate": the child understands how to communicate his or her mathematical thinking in two different ways.
13
This idea of using what the students bring to the classroom (regardless of how closely it aligns to our final goal) abandons the common deficit-based perspective, and focuses instead on an asset-based approach, which will also be a cornerstone to facilitating mathematical thinking skills.