Elizabeth M. E. Nelson
Activity #1: 10 Fruits in all
Context
This activity is designed for a Kindergarten class or beginning first-grade class. With its open-ended nature, it can be particularly useful as a type of pre-assessment to help determine what students know about decomposing numbers, how they approach solving a problem of this nature, and their perseverance. The bansho instructional strategy will be used. Considering the developmental level of the students and the possibility of multiple solutions, this activity could run from one to three days.
Objectives
I can find combinations of 10 by using objects and/or drawings (K.OA.A.3).
I can represent my solution(s) with a drawing or equations (K.OA.A.3).
Materials
Math manipulatives (including cubes or counters that are green and red, if available), blank paper, writing utensils, ten-frames, blackboard/whiteboard/chart paper/butcher paper to be used as "bansho" (optional: a big bowl, cups, grapes, and cherries).
Methods
Before problem-solving: Gather students at the rug and tell them the following story, dramatically acting it out (with realia, if preferred) or requesting that students visualize: "Last night I made a fruit salad with grapes and cherries. I mixed them all up in a big bowl. I served them in special cups. Each cup holds exactly 10 pieces of fruit. How many grapes and how many cherries could be in each cup? Find as many combinations as you can." Tell the story two to three times. Have two student volunteers retell and/or act out the story problem using their own words. Request that the rest of the class listen carefully and show whether or not they agree with the retellings. Have students turn and tell the story problem using their own words. Display the story problem on the bansho. Have students share the information they already know (There are grapes and cherries. 10 pieces of fruit.) and record this information with visuals on the bansho. Ask students what we are trying to find (How many grapes and how many cherries?) and record on bansho.
During problem-solving: Provide students with access to manipulatives, blank paper, and writing utensils. On day 1, as students are working on solving the problem, mainly focus on observing and recording different strategies and solutions that the students are using, varying levels of concrete to abstract representations being used, as well as whether or not anyone has found multiple solutions. On days 2 and/or 3, continue observing and facilitating discussion, referring the students to the bansho to avoid misconceptions or encourage perseverance. For students who continue to struggle finding one accurate solution, consider providing a container with red (cherries) and green (grapes), as well as a cup to more concretely represent the story problem. Ten frames may also be useful if children are struggling to keep track of the "fruit" or record their solutions. To help facilitate students' mathematical thinking, ask: How are you representing how many grapes and how many cherries are in each cup? Are there any more combinations? How do you know? Can you find any patterns in different combinations? How will you know when you have found all the combinations? Would there be more or fewer combinations if my cup could hold exactly 5 pieces of fruit? 12 pieces of fruit?
After problem-solving: Gather students back at the rug with their representations. Select students to share out with the group based on your observations and the needs of the students. For day 1, a beneficial discussion would be focused on the strategies students are using to find combinations or the variety of ways in which students are representing their combinations. Work with students to sort representations on the bansho by strategy used or by method of representation. Facilitate discussion in a way that leads to the summary: There are lots of [strategies I can use/ways to represent my combinations], and they all can help us solve the problem! Revisit the bansho on days 2 and 3 to remind students of previous discussions and findings. On day 2, students will likely be ready to have a discussion on finding multiple solutions and making sure they are not the same as previously found combinations. By day 3, as a class you can work together to see if anyone (individually, in pairs, or the collective class) has been able to find all of the different combinations of 10 fruits. The teacher can show an additional way to represent the combinations by using a list of sums or a T-chart of grapes and cherries. If the majority of students are ready, you may choose to work with students to put the list of sums in order (1 grapes + 9 cherries, 2 grapes + 8 cherries, and so on) and show how this ordered list can help you organize your solutions to ensure there are no repeated solutions. Record any conclusions that the class comes to on the bansho and have these records accessible for future discussions or problems that may be related to this one.
Ideas for further practice or extensions
Have each student share out one of their combinations using a complete sentence (i.e. "4 grapes and 6 cherries make 10 fruits altogether"). Give them a cup with those quantities of fruit to eat for snack or bring home to share with their families. Provide students with a similar story but with different quantities or with different objects to see how/if the students are able to extend their mathematical understanding. Provide the same story but with known quantities of grapes, so that they have to solve for the missing part.
Activity #2: Developing more efficient strategies
Context
This activity is designed for a first-grade class nearing the middle of the school year. The students should already have had significant practice with solving addition and subtraction math problems within the context of story problems and cooperative games. At this point in the year, students should also be comfortable representing and communicating their mathematical thinking and strategies used. (Please note that the example in Figure 4 shows teacher-created representations based on students' strategies and mathematical thinking observed and/or orally communicated. Ideally, the representations used will be
student-created
.) Up until this point, all of the students' strategies have been validated and valued and it is important that they continue to be throughout this lesson. However, regardless of how efficient of a strategy a student is using, this lesson seeks to help students start to think more about their criteria for strategies they select and begin to aim for more efficient strategies. An adapted form of the bansho instructional strategy will be used, as well as embedded (but explicit) vocabulary instruction. This activity will likely take up one math lesson, but can easily be repeated with different problem types or as needed to reinforce more efficient addition strategies with similar or higher numbers.
Objectives
I can represent and solve addition problems more efficiently (1.OA.A, MP5, MP8).
Materials
2 large dice, addition games, math manipulatives, blank paper, writing utensils, blackboard/whiteboard/chart paper/butcher paper to be used as "adapted bansho."
Methods
Before problem-solving: Gather students at the rug and explain to them that today we will be working on solving and representing addition problems, first looking closely at the strategies we are using. Tell them to imagine that they are playing "Addition Bingo" (or any other familiar addition game) and roll the dice record the roll so that all of the students can see. Notice how a "dull roar" ensues as students automatically begin to use a variety of strategies to combine the two numbers. To avoid students blurting out their solutions, have students explain their strategy by whispering it into their hand and holding onto it so they don't forget what they did. Explain to students that everyone is going to carefully create detailed representations of the strategies that they used and then gather back on the rug.
During problem-solving: Provide students with access to a variety of manipulatives, blank paper, and writing utensils. Circulate and observe students' representations of their strategies. Encourage students to show important details. For example, if they "used their fingers," how did they use their fingers? Did they count each set of numbers individually and then count all of the fingers in those sets one by one? Or did they use their fingers to keep track as they counted on? Which number did they count on? If any students are still struggling to represent their strategy, give them the opportunity to orally explain and/or show their strategy and have a peer or teacher create a representation of their strategy.
After problem-solving: Gather students back at the rug with their representations. Select students to share out with the group based on your observations and the needs of the students. Work with students to sort their strategies either by tool used or by strategy used. Facilitate discussion and attention to details in representations in order to ensure that all strategies are sorted appropriately.
Explain to students that we are going to focus on how efficient our different strategies are. Have them repeat the word efficient 3 times. Explain that
efficient
is a describing word that means "performing or functioning in the best possible manner with the least waste of time and effort."
24
Also tell them the student-friendly definition: "When something is efficient, it doesn't take a long time to do." Explain to students that we will do some practice using the phrases "less efficient" and "more efficient." For example, normally if I have a question for a teacher on the 2nd floor, I pick up the phone, dial her number and ask her. Would it be "more efficient" or "less efficient" for me to write the question, put it in an envelope, write her address, put a stamp on the envelope, put it in the mailbox, wait for her to get it, read it, write me back, and receive her response? That would be "less efficient" because it would take a lot more time to get an answer. Continue with 2-3 more examples worded appropriately in which the students need to respond with "more efficient" or "less efficient": varying paths to walking to the music room, writing "Connecticut" or "CT," or putting away all pencils at once or one at a time.
As soon as most students have some understanding of the meaning of "efficient," explain how we will rearrange strategies based on how efficient they are. Have students help determine how to rearrange the strategies so that the resulting display is meaningful to them. (Figure 4 portrays the resulting display from a similar lesson.) As feasible, you may choose to have students go "head-to-head" with their peers or yourself using their strategies to solve the same problem to see which is more efficient. When the class has agreed upon how to sort strategies, be sure to reinforce that all of the strategies help us get to the same solution, but that some are more efficient than others. Encourage students to try out strategies that are more efficient for the rest of the lesson and future practice.
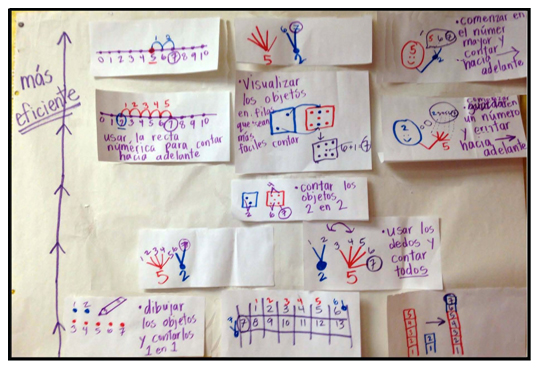
Figure 4: Example of sorting students' strategies by efficiency
Activity #3: How many toy cars?
Context
This activity is designed for a second-grade class in the last half of the school year. The students should have already had significant practice with solving one-step addition and subtraction story problems with numbers up to 100, as well as some exposure to two-step addition and subtraction math problems with smaller numbers. Students should also be comfortable representing and communicating their mathematical thinking and strategies used. Students should have had adequate experience selecting number sets that are not too easy or too difficult. An adapted form of bansho instructional strategy will be used, as well as the "just-right numbers" strategy to differentiate instruction. This activity will likely take up one math lesson, but can easily be replicated with different math problems and/or sets of numbers as needed to reinforce students' mathematical thinking.
Objectives
I can solve two-step word problems by using drawings and equations with a symbol for the unknown number to represent the problem (2.OA.A.1).
Materials
Math manipulatives, blank paper, writing utensils blackboard/whiteboard/chart paper/butcher paper to be used as "adapted bansho," a "just-right" story problem.
Methods
Before problem-solving: Gather the students at the rug and do a few quick warm-up problems that will help the students start thinking within the context of the story problem planned for the lesson: 1) Maria had 12 toy cars and 3 blocks in her backpack. How many toys did she have in her backpack in all? (no action, part-part-whole, whole unknown);
2) Jimmy had 18 toys in his backpack. There were 14 tops and some blocks. How many blocks does Jimmy have in his backpack? (no action, part-part-whole, part unknown);
3) Carla had 4 blocks, 3 tops and 7 toy cars in her backpack. How many toys did she have in all in her backpack? (no action, part-part-part-whole, whole unknown). Explain to them that today we will be working on solving and representing two-step problems. Present the following problem to students, by displaying it on the board: "Javier had 10 toys in his backpack. He had 3 blocks, 2 tops, and some toy cars. How many toy cars did Javier have in his backpack?" Have a couple of student volunteers read it out loud and others retell the story using their own words. Have students share out what is known and unknown in the story and record this on the board. If your class has worked with bar modeling to help organize information in story problems, and a student suggests it, you may wish to record:

If the majority of your class has started to successfully use and understand abstract representation, and a student suggests it, you may wish to record: 10 = 3 + 2 + ___
During problem-solving: Distribute "just-right" problem paper (see Figure 5) to students and remind them briefly that they should try to start with a problem that is not too hard, not too easy, but "just-right." Provide students with access to a variety of manipulatives, blank paper, and writing utensils. Circulate and observe as the students work to solve problems. Take note as to the strategies that they are using to solve the different problems. Some questions that can be asked to help facilitate the students' mathematical thinking include: What are you trying to find in this problem? How many blocks and tops are there in his backpack? How do you know? How can you prove it? Does your solution make sense? What if Javier miscounted and there were actually 99 toys in his backpack? How would your solution change? Are there more efficient strategies you could use to solve the problem? Is that the most efficient strategy for all of the problems? Why?

Figure 5: A "just-right" problem
After problem-solving: Gather students back at the rug with their papers and facilitate discussion based on what you observed students doing while solving the problem and based on the needs of your students. Some areas of focus may be: strategies used to organize a two-step problem, abstractly representing the problem, methods used to check your work and prove that your solution is correct. Sort and organize the students' representations based on the focus. Use "5 Productive Talk Moves" as needed to facilitate a rich discussion. Conclude by developing a summary of key concepts that the students collectively discovered and displaying them on the bansho. Allow students to record these key concepts in their notebooks or directly on their homework so that they can refer to it when doing additional practice for their homework.