Classroom activity – Classical problems
There are a number of classic problems that appear in the AP Physics B curriculum. Although the AP Physics curriculum is changing this year, a deep understanding of these classic problems is necessary to be successful in AP Physics 1. AP Physics students and Honors Physics students alike would benefit from developing problem solving skills and mastering this content. Although Physics for all focus is on the conceptual understanding and not on the algebraic manipulation, these problems can still be used for a conceptual level Physics class as a quick mathematical proof of the conceptual understanding.
Example 1: A weighted forearm
2b
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in Figure 2a below, and compare this force with the weight of the forearm plus its load.
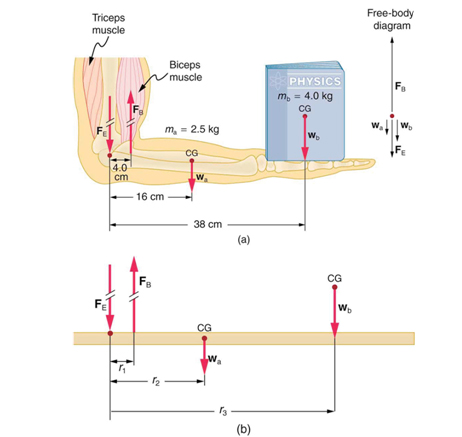
Figure 2: A weighted forearm type problem
2b
Strategy - Step 1. Draw the free body diagram (shown in Figure 2b) that shows all forces acting on the forearm (drawn simplified as a bar). Since the weight "is held" the net force and the net torque is zero. Write the two equilibrium equations and solve for the unknown.
Strategy - Step 2. Apply the condition for torque equilibrium (zero net torque). Forces
w
B
and
w
D
rotate the lever clockwise, while force
F
B
rotate the lever counterclockwise. Force
F
E
does not rotate the lever since it is acting on the rotation point. Thus the torque condition for equilibrium can be written as
w
b
x
r
2
+ w
D
x
r
3
= F
B
x
r
1
+F
E
x 0
. We know
w
B
,
r
2
,
w
D
,
r
3
and
r
1
so we can solve for
F
B
, the upward force exerted by the biceps on the forearm,
F
B
= 470 N
Strategy - Step 3. Apply the condition for force equilibrium (zero net force):
w
B
+ w
D
+F
E
=F
B
. We know
w
B
,
w
D
, and
F
B
so we can solve for
F
E
, the force at the elbow joint,
F
E
= 63.7 N
.
The ratio
F
B
/
F
E
= 7.4. The biceps muscle exerts a force that is approximately seven times bigger than the weight it lifts.
A further extension of this problem would be to calculate the maximum weight you can attempt to lift for a given upward force F exerted by the biceps on the forearm. This variation also connects to the following classroom activity, Classroom activity – Prosthetic arm. Another extension of this problem is to calculate the strength of one's biceps – inquiry lab (see Classroom activity – How strong is your biceps?).
Example 2: Standing on tiptoe
2b
A 75-kg man stands on his toes by exerting an upward force through the Achilles tendon. (a) What is the force in the Achilles tendon if he stands on one foot? (b) Calculate the force at the ankle joint. By following the procedure presented above and using the information given in Figure 8 from Reference
2b
we can solve for (a)
F
A
=2.21×10
3
N upward and (b)
F
B
=2.94×10
3
N downward.
2b
Example 3: Masseter in the jaw
2b
The masseter muscle in the jaw is attached away from the joint and enables large forces to be exerted by the back teeth. (a) Calculate the force exerted by the lower teeth on the bullet. (b) Calculate the force on the joint. By following the procedure presented above and using the information given in Figure 12 from Reference
2b
we can solve for (a)
F
1
=1.2×10
2
N upward and (b)
F
2
=84 N downward.
2b
Example 4: Head and neck lever system
2b
Due to the fact that the center of mass of the head is not directly over the pivot point in the neck but shifted towards the front, the muscles at the back of the neck should exert a force to keep the head erect. Knowing the weight of the head to be 50 N, (a) Calculate the force exerted by these muscles. (b) What is the force exerted by the pivot on the head? . By following the procedure presented above and using the information given in Figure 9 from Reference
2b
we can solve for (a) the force exerted by the muscle at the back of the neck is 25 N downward and for (b) the force exerted by the pivot of the head is 75 N upward.
Classroom activity – Prosthetic arm
A hands-on classroom activity that can be performed either before the unit or after the unit is the design and construction of a prosthetic arm. This activity is adapted from prosthetic leg activity from Teaching Engineering website.
8
Students will work in groups to design a prosthetic arm with lengths between 35 and 65 cm that will be able to lift a 5 lb bag of rice (or flour, potatoes, sand, rocks, etc). They will have to measure the minimum force of the muscle has to put in to lift the bag. An extension of the activity is to calculate the maximum weight this particular prosthetic arm can lift if the muscle force is 500 N.
Students will use the resources found in the "Resource" part below to build their own prosthetic arm. The final goal is to optimize the arm to be able to lift a 5 lb bag of rice while putting in a force load of 500 N.