There are four primary forms of catapults: the trebuchet, the mangonel, onager, and ballista.
5
Students are welcome to explore any of these forms, but this unit is written specifically for the mangonel. The mangonel is comprised of three main components: an arm, a crossbar, and a spring. The arm is a rotating device that rotates about the pivot point. At the end of the arm sits a basket that holds the projectile until launch. Students will perform experiments in which they adjust the arm length, the position of the crossbar (which controls the angle of release), and the torsion of the spring. By individually testing these three variables, students will be able to draw conclusions about how each of these components affects the trajectory.
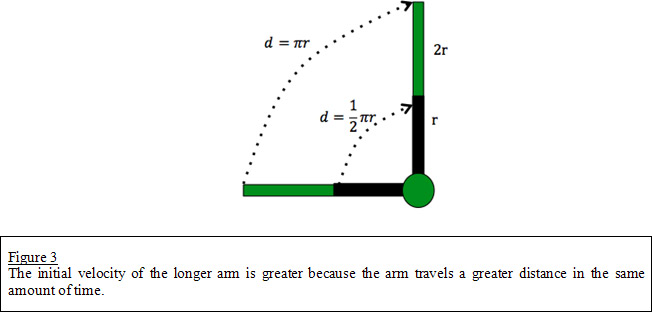
The arm length will directly affect the speed at which the projectile is launched (the initial speed). The initial speed is calculated as the distance traveled along the arc of the moving arm divided by the time it takes to move from rest to the point of launch. The longer the arm is, the greater the launch arc. An example can be seen below in Figure 3. In this figure, the arm travels a circular path, creating a 90
o
arc. Therefore, the distance traveled by the smaller black arm is calculated as
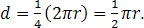
The longer green arm is twice the length and therefore the distance traveled is calculated as
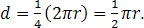
Since the arm covers the larger distance in the same amount of time as it covers the shorter distance, the initial velocity for the longer arm is greater than that of the shorter arm. The arm length also dictates the initial height of the projectile at the launch point.
Mangonels were typically used as weapons with which to destroy walls (as opposed to launching objects over walls) as they function more efficiently given smaller angles of release. Students will explore how the launch angle affects their ability to accurately predict an experimental equation for the trajectory of the projectile. The angle at which the projectile is released is dependent upon the placement of the crossbar. The projectile is released from the basket once the arm hits the crossbar. Therefore, adjusting the placement of the crossbar allows the user to adjust the angle at which the projectile is launched. Decreasing the angle of release decreases the distance the arm travels.
5
There are two types of springs: torsion and tension. For this unit, students will explore how changing the torsion of the catapult affects the trajectory of the projectile. Torsion springs are comprised of a rope or band that is twisted around the pivot point (beam). By tightening the spring, students will increase the amount of torsion, which increases the amount of force with which the projectile is launched. Loosening the spring has the opposite effect. Tightening the spring will increase the distance the projectile travels.