Heidi A. Everett-Cacopardo
Constructing Data Tables and Graphs
In order to be able to generate an appropriate graph it is imperative that the students understand the difference between the independent and dependent variables. Not all graphs follow the rule of the independent variable on the x-axis and the dependent variable on the y-axis, however this is an important piece of information that students need to master in order meet the state standards for scientific literacy and numeracy. I teach my students about the differences between the dependent and independent variables by first discussing everything that could possibly change in an experiment. The class generates a list of all of the possible variables or things that could change throughout the experiment and then I have them choose one variable that they would like to have direct control over to change between their different experimental groups. The variable they choose to change purposely becomes their independent variable. The students are then asked to decide what variable they would like to measure that would be affected by the independent variable they have chosen. The variable they have decided to measure either qualitatively or quantitatively due to their independent variable will be their dependent variable (Cothron, 2000). I inform the students that the “i” in independent can help them remember “I” have control over changing the independent variable but the “d” in dependent variable produces “data” that they measure at a result of the changes they make with the independent variable.
The students will be given the opportunity to evaluate summaries of different experiments to determine which variables described are the independent and dependent variables. This exercise will help them apply their knowledge of the independent and dependent variables. I have included a few examples of summaries under the appendix called “Examples of Independent and Dependent Variables Identification Scenarios.”
Students work hard at designing a controlled experiment but often are deficient in their ability to generate their own table to organize the data. Some labs provide a data tables already organized for the students. I believe this practice is contributing to students failing to understand the importance of the data table. A data table that effectively depicts the relationship of the dependent and independent variable is critical for a student to depict the data in the appropriate graph. Data tables provide the first step to inferring the relationship between the independent and dependent variable. I often find that students will graph a label or identifying number from a prepared data table, thinking it is the independent variable. I hope that by having them construct their own effective data tables will be better equip them to distinguish the real independent and dependent variables on their charts. The independent and dependent variables should be placed in vertical columns with additional vertical columns provided for additional calculations for the data and or labels of experimental groups. It is important for them to understand that by staying organized in constructing their data table the easier it will be to record their data and then analyze the data they have collected.
Constructing a Graph
Once the students have practiced creating an effective data table to organize the collection of their data, they will then be reintroduced to the steps of constructing a graph. It is important to ask students what graphs are and why they are used. I will have the students brainstorm in groups what they think the purpose of graphing is for and then have each groups share their ideas to the class. I hope this will create a dialogue about what purpose a graph holds for scientists and society. I want the students to understand that graphs visually represent data sets that allow quick conclusions to be made about the overall trends found within the data sets.
The first step in constructing a graph is determining what columns in the data table provide the data for the independent and dependent variables. After the independent and dependent variables have been identified, then draw and label the axes by placing the names of the independent variable on the x-axis and the dependent variable on the y-axis along with the unit of measurement that was used for each variable. I will explain to the students that they will find graphs that do not follow this rule but should understand that this will be the method that graphs are constructed in their science classes throughout high school. The next step is determining the intervals that make up the scales for the x-axis and y-axis. This is a very difficult step for the students in the process of constructing graphs. It is the most common error that I find in the graphs my students construct. I try to reinforce this difficult concept by showing them a meter stick and having them tell me about what they observe about the tick marks and the numbers represented on the meter stick. Typically, the students recognize that there is a standard distance between the tick marks and the numbers are in chronological order.
In order to provide a more tangible visual of the concept of scale, I have created a jumbo interactive graph is displayed on the wall in my classroom. I took butcher paper and made the x-axis and the y-axis using a permanent marker and placed tick marks on each axis. I then took index cards and wrote the following generic names of key parts of the graph on each index card (title, x-axis, y-axis, independent variable, dependent variable, scale, units, labels, and the numbers 1-15). I placed tape on the back of the labeled index cards and then placed them in the correct region of the graph. I go through the parts of the graph by showing the students the correct placement of the cards on the parts of the graph to provide them with a visual of all of the parts of a good graph. I make sure to focus on the scales of each axis to show them that if I make each tick mark worth 1 then the scale should read 1-15. However, if I make each tick mark worth 2 then the tick marks or intervals that divide my axis should be labeled with 2, 4, 6, 8, 10, 12, and 14.
After I have shown them a few examples of various intervals, I then “make a mistake” in dividing my scale into equal intervals and have the students identify what is wrong with my scale and how it should be fixed. I do this a couple of times with different intervals for the students to grasp the concept of scale and then refer back to my meter stick and have them compare and contrast the meter stick to the scale of my jumbo graph. I have the students draw their own example of the jumbo graph on graph paper for their notes. The next class I have after introducing my jumbo graph, I place my labels incorrectly on the graph and I call upon individual students to tell me what is wrong with my labels and where I should place them to correct the mislabeled graph. This activity provides me with insight as to how much information was retained from last class and helps to reinforce the graphing rules introduced last class. I repeat this activity all throughout the year to keep reinforcing graphing as the students easily forget their knowledge.
Spreadsheet Programs and Graphs
The business department at our high school instructs the freshman class on how to use spreadsheet programs and how to create graphs with the data sets they have entered into the programs. Due to time constraints, I will do a quick refresher lesson on using spreadsheet programs with an emphasis on transforming data sets into graphical form. I hope this review on spreadsheet programs will refresh the minds of students who already have had training and help those students who have transferred and have not received any instruction on using spreadsheet programs. At the end of the unit, under the appendix section, I have provided a tutorial on how to create graphs using a spreadsheet program (see “Create Graphs Using Spreadsheets”).
There are some important terms that I want the students to be familiar with when using spreadsheet programs. Some spreadsheet programs refer to graphs as “charts” and this could provide some confusion to students. Another source of confusion may be found with horizontal bar graphs labeled as bar charts and vertical bar graphs labeled as a column charts. The scatter plot can also be referred to as a XY chart.
Accessing International HIV Data Sets
The World Health Organization’s Statistical Information System (WHOSIS) provides health statistics on 193 countries from around the world through a database that allows you to choose various indicators from various countries. You can produce a table using the selected indicators and the table can be transformed into a line, bar, or pie graph. The WHOSIS database also allows you to download the datasets from the various indicators you have chosen and then export the data into a .csv file. This type of file (.csv) can be used in any spreadsheet program. The database is very user friendly and the web address is #18 under “Websites on HIV/AIDS Statistics.” Once you are on the web page, look under “QUICK SEARCH” and then click on “SHOW ALL COUNTRIES.” You are then within the database and can click on the various countries you are interested in then click on the “INDICATORS” tab on the top of the countries table. Choose your indicators, then click on create a table at the top of the indicator selection box. A table should appear with the countries and indicators you have chosen. Next, you can create a chart by clicking on the tab on the “CHART” tab on top of the selection box. The system will create a line graph, but in the top left hand corner, you can choose column or a pie graph. When I have the students use this website, I plan on having them first create a chart or graph using the WHOSIS system and then download the data and also produce a graph using a spreadsheet program.
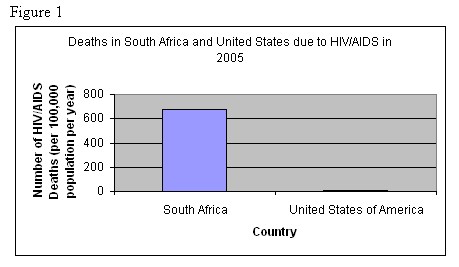
The following graph below (Fig.1) is an example of a graph I have made using the WHOSIS database using a spreadsheet program. One issue I have had with graphing the data is that the developed countries have such a small value compared to the developing countries concerning a certain indicator that the data points may not even be visible. One way to alleviate this problem is to have the students also graph the data by hand.
Types of Graphs and Charts
The next step in developing the student’s graphing skills is determining what type of graph to use when analyzing a data set. I first provide the students with notes on the various types of graphs used in science and highlight that the data they have collected or are provided with determine what type of graph to use. The main graph and chart types we will employ in the unit are bar, line, pie, map charts, and population pyramids. I will introduce and briefly review box plots and histograms but I do not have the time to have students depict data using these two types of graphs. The students will first observe examples of each of the following graphs listed below and then take notes defining the various types of graphs.
Bar Graph
Bar graphs are one the most familiar types of graphs to the students and often their first choice in depicting data graphically. The bar graph is best used for comparing a small number of groups. For example comparing different types of brands of toothpaste, favorite types of foods, number of males and females in a class, different types of fertilizer. If each group being compared is “discrete” or categorical and is not related to each other numerically then a bar graph is the most appropriate graphical display to use (Cothron, 2004, p.53). Horizontal and vertical bar graphs are both used for comparing different groups and for time series data sets. I will emphasize that we use the vertical bar graph more then the horizontal. The vertical bar graph is referred to as the column chart on some spreadsheet software programs and I will make the students aware that the column chart is also known as a vertical bar graph. There can also be double bar graphs comparing two groups at the same time. For example, a double bar graph could be used to compare, by year, the number of boys and girls playing video games over the span of a decade. Students have difficulty in recognizing there should be a uniform width to each bar they construct and space or inter space between each bar on the vertical axis. An exception to this rule would be in using a multiple bar chart (Schmid, 1983). I will provide examples of each of these types of graphs by having a sample set of data already plugged into a spreadsheet software program projected onto a screen using a LCD projector.
The stacked bar graph is used when each component of the bar represents a percentage of the whole, like a pie chart (see below). This type of graph can be visually misleading because it is difficult to determine the amount each component contributes.
Line Graph and Scatter Plots
Line graphs are also very familiar types of graphs to the students, but students typically make many errors when constructing a line graph. The line graph is best used for when the independent and dependent variables are both continuous sets of data where the intervals between each data are related numerically. In line graphs, time is usually on the x-axis. Scatter plots are frequently used in science and follow the rules of the independent variable on the x-axis and the dependent variable on the y-axis. This type of graph is appropriate for determining relationships between two variables although more then two variables can be depicted. Different data sets may also be depicted on one line graph or scatter plot. Distinctive labeling should be used to distinguish the different datasets, for example different colors or patterns (Schmid, 1983).
Histogram
Histograms, also called frequency charts, are visually related to the vertical bar graph. Data sets that deal with frequency and distributions are best simplified by determining the number and size of the class intervals or bins. Once this has been determined, “count the number of data points in each interval, and plot the counts as bar lengths” (Chambers, 1983, p.24). Determining the class interval or bin size is critical in depicting the data appropriately. Data can be lost if too large of a bin size is chosen when constructing a histogram and choosing a bin size that is too small can produce a cluttered display with too many intervals that may not even contain any data points (Schmid, 1983). This type of graph is the basis for a population pyramid, which is one of the main graphical displays used to study population dynamics.
Population Pyramids
Population pyramids or age structure diagrams are the best graphical display for comparing the sex and age distribution of a population. This graphical display is constructed using a paired horizontal bar graph. Each age range is given a bar in chronological order starting with birth at the bottom. The length of the bar corresponds to the percentage of the population that makes up a certain range. These types of graphs are also helpful in predicting the type of growth a population can expect for a population’s trends in age and sex distribution (PA Dept. of Health, 2001).
Pie chart
Pie charts are used for depicting discrete categories that are part of a whole. A data set looking at the percentage of the entire population of men, women, and children infected with HIV would be appropriately displayed with a pie chart. Pie charts can visually mislead the observer how to what percentage of the pie each category takes unless the percentage values are included in the graph. Pie charts are best used with data sets containing less then eight groups (Schmid, 1983).
Map chart Choropleth Map
Map charts or choropleth maps are used for depicting a data set that is spatially distributed over an area. A data set looking at the number of HIV cases found within each state is an example of data appropriately displayed using a choropleth map of all fifty states. The various shades used to color in each state could indicate different ranges of values of HIV cases within each state. The darker shaded areas could indicate values. Start by determining the range your values cover and then divide the range into the number of categories you wish to depict. Usually on three, four, or five groups are best. A greater or lesser number of groups can obscure the data.
Misleading Graphs and Charts
There are many types of graphs and charts that when used correctly provide a visually engaging and appropriate summation of the relationships that certain data sets hold. Although graphs can communicate more effectively than a data table, they can also mislead and shroud the actual relationships or trends. Minute details like absent labels on the axes and the inappropriate scales are some common errors (Schmid, 1983). Choosing the wrong graph or chart type can easily destroy effective communication of the data. An example would be using a pie graph for a data set containing more then eight categories. Another example would be choosing bin sizes that are so large that certain data points end up being lost. Pie graphs are more decorative and should not be used to precise data due to the difficulty in assigning a precise percentage of the slice. These various points will be highlighted throughout the section on graphing and review of the various types of graphs and when to use them.
Introduction to Epidemiology & HIV/AIDS
Epidemiology is the study of the spread of diseases throughout a population. Epidemiologists focus on determining when a disease appears in a population, the mode of transmission, and where the disease spreads to in a population (Tortora, 2002). This field of biology focuses on many factors that are related not only to the origin and spread of disease but also the way in which people are affected by the disease. Some important pieces of information or data that an epidemiologist collects on a member of a population deal with the age, sex, occupation, personal habits, socioeconomic status, and history of immunizations. The following are key terms that students need to know the definitions of: etiology, prevalence, incidence, and mortality rates. Etiology is defined as all the variables that are considered as factors in causing disease in an individual (Philips, 2001). Incidence refers to the “number of new cases” of disease that take place over a certain amount of time, for example the number of HIV infections during the year 2001 (Phillips, 2001, p.10). Prevalence is similar but counts the number of cases already present in a certain population over a period of time. Mortality or morbidity rate is the number of deaths that take place during a year (Phillips, 2001). This vocabulary is important for the students to understand when analyzing the data sets provided on the World Health Organization statistics web page called WHOSIS.
Comparing and Contrasting Populations
My students will have already received instruction on the criteria used to determine whether a country is developed or underdeveloped based on the shape of a country’s population pyramid. I will remind them that the shape of developing country has a very wide base. This wide base indicates a large portion of the population is composed of very young age groups and as the age increases, the trend is each age groups shrink in size. The developing country’s population pyramid tends to narrow with increasing age. The narrow top of the pyramid indicates very few older people make up the population indicating a very low life expectancy for individuals in this population. Botswana is a country that has a population pyramid with a wide base and narrows toward the older age groups.
The shape of a population pyramid from a developed country will have either a narrow base due to fewer younger people in the population and or the overall shape ends up resembling an irregular block due to each age groups being composed of roughly the same amount of people (PA Dept. of Health, 2001). United States is a country that has a population pyramid with a blockish shape due to the large middle age portion of the population. Developed countries have larger percentages of their population aging and this provides the more blockish shape in comparison to the pyramid shape of the developing country. Various examples of population pyramids I am describing can be found at website #10 listed under “Websites with Population Statistics.”
I often find my students tend to overlook the units of a number as an unimportant detail. I tell the students to pay attention to the units (for example, thousand versus millions) that describe the population of a country by showing them a pyramid from a country with a small population (ex. Jamaica) with a country with a very large population (ex. China). I want to make sure the students understand that critical values are the percentages of a population that fall in various age groups rather than the absolute number.