Lesson 1: What is Income Inequality?
An introductory lesson to the curriculum unit will have statistics students examining three different pie charts on Kahoot, a phone application that enables teachers to poll or quiz their students. Teachers can then view the results. The first pie chart would represent an even income distribution, with 20% belonging to each of the top quintile, second quintile, third quintile, fourth quintile, and bottom quintile. The second pie chart would represent an income distribution that is a little less equitable, and the third pie chart would represent a far more inequitable income distribution. The students will be instructed to select the pie chart that they believe reflects the distribution of income in the United States. Following their selection, they will need to justify on paper which chart they picked and why. They will be invited to share their justifications out loud after.
Next, students will be presented with graphs that illustrate the uneven distribution of income in the United States. Students can use the graph in Figure 1 to answer the following questions. These questions are meant to assess their prerequisite knowledge of how to gather information from a bar graph, describe its shape, and draw conclusions accordingly. Students will be asked to volunteer their answers out loud after.
-
The bar graph explores the relationship between which categorical variable and which quantitative variable?
-
How would you describe the shape of the data distribution? Is it left-skewed, right-skewed, unimodal, symmetric, or random? Does the distribution favor any group of people?
-
About how many times greater was the Top 0.1%’s average income than the Bottom 90’s average income in 2015?
-
Based on the bar graph, does income inequality exist for people at the top of the income distribution? Justify your reasoning mathematically.
-
Which types of jobs would you expect people in the Top 0.1% to have?
-
Which types of jobs would you expect people in the Bottom 90% to have?
-
Why do think a graph like this is useful to us in the real world?
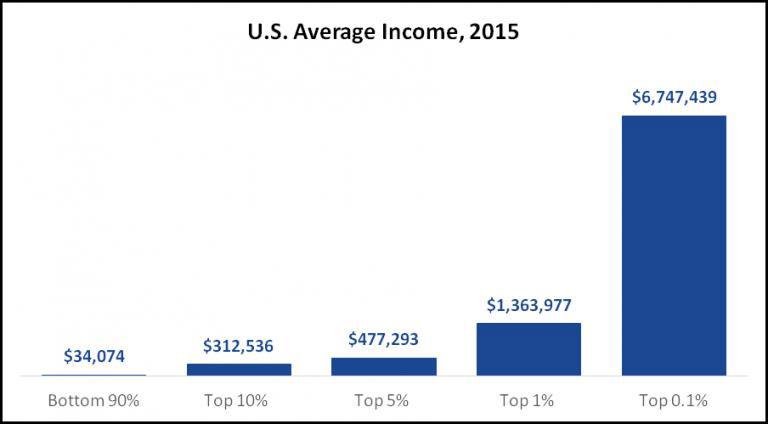
Figure 1: Average Income For Various Income Brackets in the U.S. in 2015 (36)
Figure 2 will expose students to a line graph. Students will use the graph to answer the questions during a whole-group discussion:
-
How has the Top 1%’s share of total U.S. income changed from 1913 and 2015?
-
During what year has the Top 1%’s share of total U.S. income peaked? Why do you think this is?
-
The Top 1%’s share of total U.S. income seems to have declined until about the 1970s. Why do you think this is?
-
The Top 1%’s share of total U.S. income seems to increase overall from the 1970s onward. Why do you think this is?
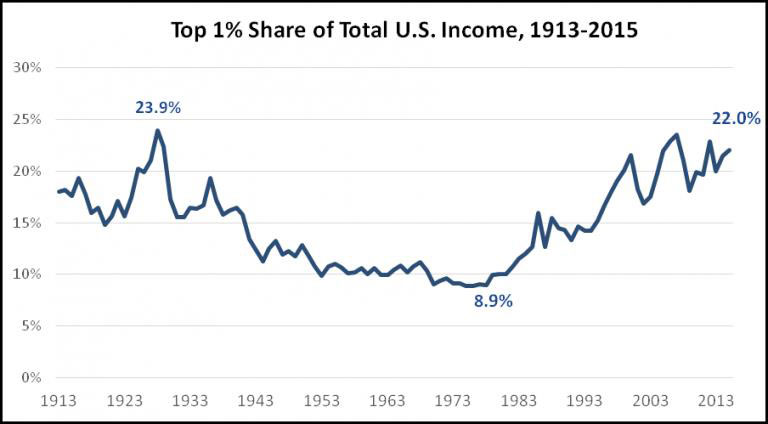
Figure 2: The Top 1%’s Share of Total U.S. Income from 1913 to 2015 (37)
After examining both the bar graph and line graph, student will revisit the pie charts presented to them at the beginning of the lesson. They will be asked if they would change their initial choice of the chart that reflects the income distribution in the United States. Finally, they will be exposed to the correct chart (the pie chart that is most inequitable) via a PBS News Hour video called “Land of the Free, Home of the Poor,” which might surprise them.
38
Once the video is finished, students will be exposed to the class results for the pie chart poll. They will then need to answer the following questions for a post-video discussion.
-
Why do you think the survey participants underestimated the level of income inequality in the United States?
-
The low-income workers in the video were able to accurately identify the pie chart that represented the distribution of income in the United States. Why do you think they were able to make the correct choice?
-
Do you think it’s disconcerting that so many Americans are unaware of the extent to which income inequality exists in the United States?
-
Why do you think income inequality might be considered a problem?
Lesson 2: Using Linear Regression to Determine Which Factors Correlate with Income Inequality
Students will be alerted to the fact that income inequality is a global concern as well as a domestic issue. As a warm-up activity, students will be split into small groups. Each group will be required to list as many possible causes of income inequality as they can. Among the causes they list might be historical disenfranchisement of minorities, differences in education levels, and unfair compensation for labor. The teacher might also need to use guiding questions to prompt students for the less obvious answers like technological growth, declining unionization rates, tax systems, or globalization. Once students share their listings aloud, the teacher will need to explain that before we can alleviate income inequality, we need to know which factors contribute to the problem. One of several ways to do this is to see which causes have a linear relationship with income inequality. The method we will use to do this is called linear regression.
A linear regression model allows us to predict output values for different input values of our independent variable. It is in the form , which is slope-intercept form. We use the carat mark on top of the for a linear regression model to indicate predicted output value as opposed to a theoretical output value. The slope, , tells us how much the dependent variable increases or decreases for each one-unit increase in the independent variable, x. The y-intercept, , tells us the value of the dependent variable when the independent variable takes on a value of zero. Students can attempt to fit a trend line to a scatterplot using a ruler and determine the equation of this line by hand, but this unnecessary because the TI-84 Plus graphing calculator allows us to perform these tasks with more ease.
The correlation coefficient, denoted by the letter r, gives us information about the strength and direction of the linear relationship between the independent and dependent variables. The correlation coefficient is always a value from -1 to 1. If r is negative, this indicates that as the value of the independent variable increases, the value of the dependent variable decreases. If r is positive, this indicates that as the value of the independent variable increases, so does the value of the dependent variable. A correlation coefficient of zero indicates that there is no linear relationship between the independent and dependent variables. A correlation coefficient of -1 or 1 indicates a perfectly linear relationship between the independent and dependent variables. However, it is important to note that just because two variables are highly correlated, this does not mean that one causes the other. There are outside factors called confounding variables that can influence the linear relationship between two variables. The coefficient of determination, given by r
2
, is simply the correlation coefficient multiplied by itself. It gives us the percentage of variation in the dependent variable explained by the independent variable. The coefficient of determination is always a value from 0 to 1.
The teacher will need to walk the students through an example of a problem involving linear regression. Suppose we want to come up with a model that can predict the average SAT math score of a state given the Gini coefficient of that state. Suppose further that we want to know whether or not there exists a strong linear relationship between the Gini coefficient of a state and the average SAT math score within that state. The teacher will first have to give students an overview of what a Gini coefficient tells us about the income inequality level of a specific location. After, students will examine the data table below.
Table of Gini Coefficients and Average SAT Math Scores of Twenty-Two States
(39)
|
State
|
Gini Coefficient
|
Average SAT Math Score
|
|
Utah
|
.419
|
614
|
|
Alaska
|
.422
|
533
|
|
New Hampshire
|
.425
|
520
|
|
Wisconsin
|
.430
|
649
|
|
Idaho
|
.433
|
493
|
|
Maine
|
.437
|
499
|
|
Minnesota
|
.440
|
651
|
|
Washington
|
.441
|
534
|
|
Vermont
|
.444
|
551
|
|
Oregon
|
.449
|
548
|
|
Ohio
|
.452
|
570
|
|
Arizona
|
.455
|
553
|
|
Arkansas
|
.458
|
594
|
|
Virginia
|
.459
|
541
|
|
Pennsylvania
|
.461
|
531
|
|
New Jersey
|
.464
|
526
|
|
Rhode Island
|
.467
|
524
|
|
Texas
|
.469
|
507
|
|
California
|
.471
|
524
|
|
Massachusetts
|
.475
|
551
|
|
Connecticut
|
.486
|
512
|
|
New York
|
.499
|
523
|
Students will be required to use the TI-84 Plus to determine the linear regression model, correlation coefficient, and coefficient of determination for the data. They will be supplied with the following instructions:
-
After turning on the TI-84 Plus, hit [STAT][EDIT][1][ENTER].
-
Enter the data for the Gini coefficient (the independent variable) into L1 and the data for the average SAT math score (the dependent variable) into L2.
-
Hit [STAT] [CALC][4].
-
Next to Xlist, input L1. Next to Ylist, input L2. Then scroll over the word “Calculate” and press [ENTER].
-
You should see the values of a, b, r
2
, and r. To determine the linear regression model for the data, plug in the values of a and b into the equation y = ax + b.
When one follows the above procedure, one will obtain the linear regression model for the data: = -709.60x + 86.76. Students at this point should provide answers to the questions below.
-
How does the sign of the correlation coefficient relate to the sign of the slope?
-
Interpret the slope of the model in the context of the data.
-
Interpret the y-intercept of the model in the context of the data.
-
What is the value of the correlation coefficient, and what does this tell us about the form, direction, and strength of the linear relationship between a state’s Gini coefficient and average SAT math score?
-
Use the linear regression model to predict the SAT math score of a state with a Gini index of .468.
-
Use the linear regression model to determine the Gini coefficient of a state with an average math SAT score of 650. What do you notice happens? Why is this a problem?
-
Does this model seem practical to you in a real-world context? Why or why not?
Next, students can create a scatterplot of the data by following the instructions below.
-
Hit [2
nd
][STAT PLOT][1].
-
Make sure Plot1 is the only plot that is turned on.
-
For Type, select the first option, which is the scatterplot.
-
Next to Xlist, input L1.
-
Next to Ylist, input L2.
-
Next to Mark, select the first option (which displays each ordered pair as a point).
-
Hit [ZOOM][0].
-
Press [GRAPH] to view the scatterplot.
Some questions to ask the students about the scatterplot are listed below.
-
Looking at the scatterplot, does the association between the Gini coefficient of a state and the state’s average SAT math score appear to be positive, negative, or completely random?
-
Does the scatterplot appear to be linear to you?
-
Which states appear to have particularly high SAT math scores? Why do you think this is the case?
The scatterplot for this data allows the teacher to address that in the real world, most data is not perfectly linear. The correlation coefficient for the data is -.34, which indicates that a linear relationship exists between the Gini index and the average SAT math score of a state. This linear relationship is weak, since the correlation coefficient is closer to 0 than it is to -1. The regression equation tells us that for every one-unit increase in the Gini coefficient, the SAT math score of a state decreases by 709.60 points. This is not exactly useful information considering the Gini coefficient cannot be lower than 0 or higher than 1. The data equips the teacher with an opportunity to discuss extrapolation, the process of estimating the value of a variable or function outside an observed range. If one tries to use the regression model to estimate the Gini coefficient of a state with an average SAT score of 650, one will discover that the estimated Gini coefficient is negative. However, a Gini coefficient can never be negative. The moral of the story here is that the usability of a linear model can be limited. This data allows room for a discussion of confounding variables. Some states (like Wisconsin or Minnesota) might have unusually high average SAT math scores because the SAT is not a required test for their students. These states require the ACT instead, and those who take the SAT tend to be the most ambitious students. However, when the correlation coefficient of a scatterplot indicates a strong linear relationship between an independent and dependent variable, the linear regression model can help us effectively make predictions given specific input values.
Another tool that allows us to assess whether a linear model is an appropriate fit for a data set is a plot of residuals. A residual is the difference between the predicted y-value () and the actual y-value (y). The residual plot is a scatterplot of each (x-value, residual) ordered pair. A plot of residuals can be created quickly using the TI-84 Plus graphing calculator. The steps, which will be reviewed with the students for the SAT example, are outlined below.
-
Press [Y=] to deselect the stat plots and functions.
-
Press [2
nd
][Y=][2] to access Stat Plot 2 and enter L1 next to Xlist.
-
Enter the Ylist by hitting [2
nd
][STAT] and using the up and down cursor keys to scroll to RESID.
-
Press [ENTER] to insert the RESID list.
-
Press [ZOOM][9] to access the plot of the residuals.
If all the points look randomly dispersed around the x-axis, then this tells us that a linear model is appropriate for our data. Otherwise, another type of model (i.e. exponential, logarithmic, etc.) is a better fit. The residual plot for the data is somewhat random, but does not resemble a cloud of points evenly scattered around the horizontal axis. This plot is consistent with the correlation coefficient, which suggests that a linear relationship exists between the average SAT math score and Gini coefficient of a state. However, this relationship is far from perfect.
After students are introduced to the graphing calculator functions associated with linear regression, they will work on a project that will have them picking a variable that potentially influences income inequality. They will have to find data that quantifies this variable using a website such as the World Economic Forum or World Inequality Database. They have the freedom to use data relating to states within the country or several different nations. Their goal will be to find out if a linear relationship exists between the variable of their choosing and the Gini coefficient of a state or nation. They will need to do the following in the form of a written report.
-
Specify the independent variable and dependent variable in your study.
-
Create a scatterplot of your (x, y) ordered pairs by hand or using a program like Microsoft Excel. Title the scatterplot and label the axes with the appropriate units and variables.
-
Use the TI-84 Plus to determine the equation of the linear regression model, in slope-intercept form, for the scatterplot.
-
Interpret the slope and the y-intercept of the linear regression model in the context of the data.
-
Find and interpret the correlation coefficient and coefficient of determination in the context of the data.
-
Create a plot of residuals for the data by hand or using a program like Microsoft Excel. Does this plot suggest that a linear model is appropriate for the data? Why or why not?
-
Are there any political policies that might have caused the value of your variable to be higher or lower for certain countries? Include any interesting statistics related to these policies. Also include and interpret any graphs or charts that might allow us to understand the impact of these policies.
-
For countries that are adversely affected by the variable, what policies do you think should be put into place to alleviate income inequality?
There will also be an oral presentation component to this project that should be no longer than eight minutes. Students will be required to use some type of visual to summarize their answers to the focus questions. This can be a PowerPoint presentation, video, poster board, or any other approved visual. While students are presenting, their classmates will be required to fill out questionnaires describing any new insights or facts they learned from the presentation and explaining why they agree or disagree with the presenters’ proposals for alleviating inequality.
As an example of a project, students might decide to see if a linear relationship exists between a country’s minimum wage and the Gini coefficient of that country. The group would be advised to select forty to fifty countries with varying levels of income inequality. Then, they would have to research the minimum wages of these countries in United States dollars using a website such as the World Economic Forum to gather the data that they will analyze for their written report. They would need to use the TI-84 Plus or statistical software to come up with the scatterplot, residual plot, regression model, correlation coefficient, and coefficient for the data. They would be required to research policies or factors that have influenced the minimum wage in various countries. They might decide to examine a graph of how the minimum wage in the United States has changed over time and compare to a similar times series graph for another nation. Based on factors or policies that have affected the minimum wage in different nations, they would need to come up with their own proposal for increasing the minimum wage in countries where it is relatively low.