Timothy J. Chiaverini
Lesson 1: Density
Scientific Objectives
|
1.
|
Describe the relationship between mass, volume and density.
|
|
2.
|
Explain how an object's density determines whether it will sink or float.
|
-
Mathematical Objectives
-
|
3.
|
Construct graphical models of real-world data.
|
|
4.
|
Find and describe the equation of a line in slope intercept form.
|
|
5.
|
Compare and order numbers and use proportional reasoning to solve problems.
|
Materials Needed
For this lesson, students will need a 100 mL graduated cylinder, 50 mL of water, 50 mL of Vegetable Oil and 50 mL of Alcohol. Students will also need a graphing calculator, graph paper, pencils, rulers, and balance scale (preferably a digital scale). The teacher will need a large, transparent container such as a fish tank filled with water in the front of the room where all students can see it. The teacher will also need one can of diet cola and one can of regular cola, and a computer with an internet connection.
Suggested Tasks/Strategies
Students will begin the lesson in pairs. Pose the following question to the class as a whole: What determines whether or not an object will sink or float? Let students discuss this question in their pairs, and inform them that they will share their answers with the whole class in 5 minutes. Most students will have the popular misconception that mass is the deciding factor in whether or not an object will sink or float. Display students' answers to the opening question, and show an excerpt of the YouTube video: "Buoyancy and Density," from Science Online. To access the video entitled Buoyancy and Density, go to http://hilaroad.com/video/sink_float.html and select "low resolution preview."
Show from the 1:14 mark to the 7:50 mark.
There are various concepts covered in the video that should be reiterated to ensure student understanding. The following questions can promote productive discourse and classroom discussion: How can we calculate the density of an object? Why does a cruise ship float while a pebble sinks? In general, what are the most important things to consider in determining whether or not an object will sink or float? Since the density of water is calculated in the video, it may be unnecessary to have the class calculate the density of water. However, the teacher may choose to not show that portion of the video and have students find the density of water by calculating mass and volume using a graduated cylinder and a scale.
Ask for a pair of volunteers and provide one of them with a can of cola and the other with a can of diet cola. Ask this group to predict what will happen if both cans are immersed in the same tub of water. Will they both sink? Will they both float? After students make their predictions, have the volunteers drop the cans into the clear water receptacle. As a whole class activity, calculate the densities of the two cans and discuss why the regular cola sinks, while the diet cola floats.
Following this discussion, students will work in pairs. They will begin an experiment to find the densities of three fluids, for example: vegetable oil, salt water and alcohol. They will do so by calculating the densities of the fluids. Students will construct a scatter-plot where mass is the dependent variable and volume is the independent variable for each of the fluids. For each fluid, students will collect five mass measurements that correspond to volumes 0 mL, 10 mL, 20 mL, 30 mL, 40 mL and 50 mL to generate ordered pairs and plot the ordered pairs on their scatter-plot. Be sure to model finding the mass of the fluids by subtracting the mass of the empty cylinder (this is demonstrated in the video).
Students will calculate the densities of the fluids by drawing a line of best fit on their scatter-plot. They will find the equations of each line of best fit. The slope of the line of best fit will be the density of the fluid in question. At the teacher's discretion, the graphing calculator may be used to create the scatter-plots and a linear regression to find the equations of the lines.
Students should be assessed based on their ability to solve word problems and answer conceptual questions related to density. Students should be adept at using the symbolic formula for density and should be able to find the density of fluids and objects using their mass to volume ratios.
Lesson 2: Buoyant Force
Scientific Objectives
-
|
1.
|
Define buoyant force and explain Archimedes Principle.
|
Mathematical Objectives
-
|
2.
|
Construct appropriate symbolic mathematical models to fit real world data.
|
|
3.
|
Calculate buoyant force, mass, volume, and density using symbolic models.
|
Materials Needed
Two liters milk, a two liters of soda (not diet) and two liters of fresh water. (The amount and type of fluid needed for the experiments may vary, depending on the preference of the teacher and the number of students in the class). Each group will need three dense solids that will sink in all three liquids and can be hooked up to a spring scale. Suggested dense solids include one right cylinder, one sphere and one right rectangular prism. In addition each group will need and one right rectangular prism of solid wood and a centimeter ruler. Each group will need a spring scale and a wide-mouthed graduated cylinder tall enough for each solid to be completely submerged.
Suggested Tasks/Strategies
Students will work in pairs for this lesson. Ask students to place their block of wood into the fresh water. One student should push down on the block of wood. To reinforce previous material, have the class briefly discuss why the block of wood does not sink in the water. Ask the class to recall the density of fresh water, and as a whole class, calculate the density of the wood. Find the mass of the block using the spring scale and calculate its volume using the following equation, where m = mass, d = density and V = volume: d = m/v.
Ask students to place the block of wood in the water again. Ask students to push down on the block of wood until it is completely submerged. Students may notice that the block is "pushing against" their hand as they try to keep it submerged. Tell students that today, they will learn about this force that is pushing against them to keep the block of wood afloat. Show an excerpt of the YouTube video: "Buoyancy and Density," from Science Online. Show from the 7:50 mark to the 9:29 mark. To access the video entitled Buoyancy and Density, go to http://hilaroad.com/video/sink_float.html and select "low resolution preview."
During the video, display Archimedes' Principle in front of the class. Following the video, discuss the role Archimedes' Principle plays in keeping the wood block afloat in the water.
It should be noted that following the video, students may also need a refresher and some examples on using the formulas for volume of solids, specifically the formula for spheres: V = 4/3 φ r
3
, and Right Cylinders: V = φ r
2
h. Students may also need an example to remind them how to calculate the weight of an object on earth. For W = weight on earth, m = mass and g = the gravitational constant: W = mg.
Significant time should be spent explaining and discussing relationships that lead to an understanding of buoyant force. Since buoyant force is the weight of the water that is displaced by a submerged object, students need to be able to calculate the volume of their solids in cubic centimeters. The following symbolic understanding of buoyant force is necessary to conduct the experiment:
Given the following:
m
a
is the mass of the object in air
m
f
is the mass of the object submerged in the fluid
m
d f
is the mass of the displaced fluid
F
b
is buoyant force exerted on the submerged object
g is the gravitational constant
d
f
is the density of the fluid
The mass of the displaced fluid can be found by subtracting the mass of the submerged object from the mass of the object in air, and m
d f
= m
a
m
f
(This reinforces the fact that buoyant force is actually a net force, and could lead into a discussion of neutral buoyancy, where the weight of the object is equal to the weight of the fluid displaced).
The relationships listed above yield F
b
= m
d f
g = (m
a
m
f
)g. Since the volume of the object is the same as the volume of the displaced fluid when the object is fully submerged,
d
f
= m
d f
/V and d
f
V
= m
d f
. Using substitution, this yields d
f
= (m
a
m
f
) / V
The teacher can now design an experiment where students can use the spring scale to calculate each object's mass when submerged in fluid and when suspended in air. The ability to measure the dimensions of each object with a centimeter ruler allows students to calculate the volume of spheres, cylinders and rectangular prisms using their formulas. With this information, students can calculate the density of each fluid.
Following the experiment, students should spend time solving word problems and answering discussion questions which reinforce the concept of buoyant force and bolster their comfort level with the symbolic representations and formulas. CAPT-like questions including grid-in and open-ended examples are suggested.
Lesson 3: Sea Level Rise and the Relationship between Temperature and Volume
Scientific Objectives
|
1.
|
Explain the relationship between changes in temperature and changes in volume and density.
|
Mathematical Objectives
-
|
2.
|
Use mathematical models to make predictions about real-world phenomena.
|
|
3.
|
Construct graphs of real-world data and analyze data using graphs.
|
|
4.
|
Find the equation of a quadratic function given its tabular and/or graphical model.
|
Materials Needed
A classroom set of glass graduated cylinders with the ability to measure volume in 1/10 mL increments, markers, ice cubes, and a large tub or jug full of fresh water. Graphing Calculators and computer with an internet connection.
Suggested tasks/strategies
At the opening of the lesson, students should be provided with a graduated cylinder or beaker filled approximately halfway with water. Students should place 3-4 ice cubes in their cylinders, and mark the water level on the beaker. The teacher should ask students what they think will happen to the water level when the ice melts. Classroom discussion should center on the central question: will the water level rise? How much will it rise? How much water is displaced by the ice and can it be calculated? The ice cubes will be left to melt at room temperature. Have students record their predictions on a worksheet about the water level.
At this time, students should view the PBS video "Extreme Ice." This video can be found online at http://video.pbs.org/video/1108763899/. The video takes approximately 50 minutes. Following the video, students should observe how the water level changed when the ice melted in the beakers. As a class, discourse should center on how the results would have been different if the ice were melted separately from the water, and then the melt water were added to the beaker. Students should make the connection from the experiment to the difference in impact on sea levels between sea based melting--ice and land--based melting ice.
Some critical questions:
If it melted, which ice would have a more significant impact on global sea levels, land-based ice or sea-based ice?
How does the reduction in snow and ice cover on land and on the sea affect the amount of sunlight that is absorbed by the oceans and the land?
How do particles create "dirty snow or ice" and how does this phenomenon affect the impact of the sun on melting ice?
Following this sequence, ask students to consider what would happen if the oceans absorbed more and more sunlight. Is there another factor contributing to sea level rise? Is there some reaction that might take place if the oceans were absorbing more heat from the sun?
Students will be provided with a table of data
15
(see the table below). The data will contain values for temperature and volume changes for 1 mL of fresh water.
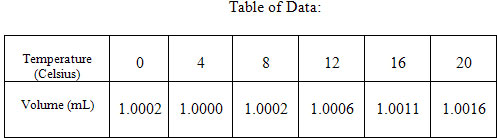
Students should use this data to find a quadratic equation that models volume of 1 mL of water as a function of temperature. Students may use the quadratic regression feature of the graphing calculator to find the quadratic equation. Students should then use their equations to predict how much the volume of the water will increase as the temperature increases to 24 and 28 degrees Celsius. The accuracy of this quadratic approximation can be discussed. Teachers may wish to ask students if they believe this quadratic function will become a more or less accurate predictor of volume as temperature increases. Students could calculate the volume at 100 degrees Celsius using the function and compare it to the measured value of the specific volume of water at 100 degrees Celsius. They will discover that the function is not accurate at high temperatures.
Lesson 4: Thermal Expansion and Convection
Objectives
-
|
1.
|
Design a hot air balloon that uses convection as an engine.
|
|
2.
|
Research renewable energy sources that employ convection currents
|
-
Materials Needed
-
Dry cleaner bags, flexible straws, thin birthday candles, aluminum foil, a lighter, scotch tape, exacto knives and scissors
-
Suggested tasks/Strategies
The lesson will begin with students viewing the final segment of YouTube video: "Buoyancy and Density," from Science Online. To access the video entitled Buoyancy and Density, go to http://hilaroad.com/video/sink_float.html and select "low resolution preview."
Students should discuss the following important questions before creating their hot air balloons:
Some critical Questions
How does a hot air balloon fly? What role does thermal expansion play in the engine of a hot air balloon?
Why does a helium balloon float and how does the density of the air inside of a hot air balloon change as it is heated up?
What happens to the mass of the air inside the balloon? How about the volume?
For this culminating activity, students will be divided into groups of three. Each group will design a homemade hot air balloon. The instructions on creating a hot air balloon are located in the resources section. Teachers can decide for themselves how to use the exciting process of creating a hot air balloon. Some suggestions might include varying the size of the bags used, and the number of candles in the engine. Unless the hot air balloons are teathered, it is suggested to fly them indoors to prevent runaway ballons that can cause fires and other problems.
Teachers could extend the lesson by having students use the Ideal Gas Law to calculate the density of air. This could be used to compare the density of hot air in the hot air balloon with room temperature air outside the balloon. Rearranging PV = nRT gives: density = m/V = MP/RT, where m = mass of the air in a volume V and M is the molar mass of air (roughly 28 gm/mol since 80% of air is nitrogen gas which has M = 28 gm/mol). Using 300 K as room temperature, 1 atm as the pressure and R = 82.05 cm3 atm/mol K, one obtains the density of air as approximately 1.22e--3 gm/cm3. By using the temperature of hot air, you could also calculate the density of hot air, and from this the buoyant force for a hot air balloon.
For a culminating assignment, students will research solar chimneys. Students will write a paper detailing the history of solar chimneys and describe how they work. In their research papers, students should connect what they have learned about buoyancy, density and thermal expansion to the operations of a solar chimney.