The mathematical equations that relate the properties of an ideal gas will be presented in this section. The properties of actual gas samples with low densities led the concept of an ideal gas. If a gas is compressed while keeping its temperature constant, the pressure increases. Similarly, if a gas expands at constant temperature, its pressure decreases. That is, pressure and volume are inversely related at a given temperature. To a good approximation, the product of the pressure and volume of a gas sample that has a low density is constant (PV = constant) at a constant temperature. This result was discovered experimentally be Robert Boyle (1627- 1691), and is known as
Boyle’s Law.
Another way to define Boyle’s law is the following postulate:
At a
constant temperature (T= constant)
, the volume of the gas decreases as the pressure increases
P
1
V
1
= P
2
V
2
or equivalently
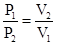
Since the temperature remains the same, a decrease in volume would result in increased gas pressure, as depicted in the following illustration (where “isothermal” means “constant temperature”).
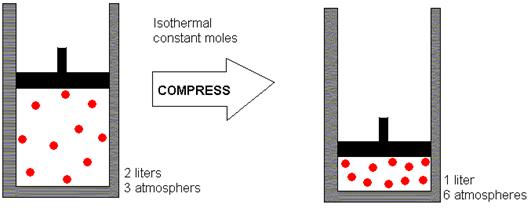
Source: http://dlrgenchem.com/LECTURES/Gaslaw.htm